2635. Detonating cord

In a beautiful sunny day Hedgehog was walking on his favorite meadow. However, he saw something unusual, that was not there before. From the distance it looked like a tangle of ropes. However, coming closer to untangle it and studied the material from which it is made, the Hedgehog came to the conclusion that this is a fuse.

Taking a good look at it, the Hedgehog came to the conclusion, that one who made it, was boring and he had a lot of free time, because the cord was tangled, and had a huge amount of knots! After careful reviewing, it was found out that there are n knots (nodes) and m connections between them. Each connection connects two nodes and burns evenly. When a node is ignited, all connections that contain it light up.

However, Hedgehog did not like the thing he found, and he decided to destroy it. To do this, he decided to use a match that was so conveniently lying in his pocket. He can set fire to one of the nodes, and the whole structure starts to burn. The hedgehog is a busy smesharik, and wants to burn this structure as fast as possible. Help him to determine which node must be set on fire for this.

Input. The first line contains two integers  n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ n * (n – 1) / 2) – the number of knots and ropes between the nodes, respectively.

Next m lines contain the description of connections between the nodes – three integers a_i, b_i and t_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i, 1 ≤ t_i ≤ 1000) – the numbers of nodes that the i - th rope connects and in how many seconds this rope will completely burn out, being set on fire from one of its ends.

Maximum one rope connects each pair of nodes. It is guaranteed that the entire cord can burn if any of its knots are set on fire.

Output. Print the pair of numbers – the node number, which should be set on fire, and how long the whole cord will burn.

Sample input	Sample output
4 4 1 2 3 2 3 4 1 3 5 1 4 1	2 4

SOLUTION

graphs – Floyd - Warshall

Algorithm analysis

Let g be the distance matrix of a given graph. The weight of the graph edges equals to the burning time of the ropes. The entire cord can burn out, so graph is connected. Find the shortest distances between all pairs of vertices using the Floyd-Warshall algorithm.

If we set fire to a knot (vertex of the graph) v, then the entire structure of the ropes will burn out after a time equal to the distance from vertex v to the farthest vertex. It remains to find the vertex, the distance from which to the farthest is minimal.

Example

Below given a graph from a sample and a matrix of shortest distances.

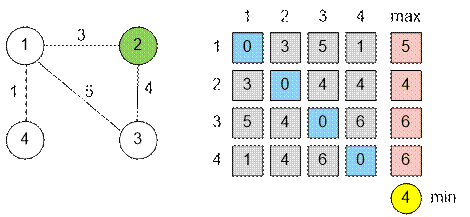
When vertex 2 is set on fire, all other vertices will burn out the fastest, in 4 seconds.

Algorithm realization

Store the distance matrix in the array g.

#define MAX 102

int g[MAX][MAX];

Read the input data. Build a graph g. Vertices are numbered from 1 to n.

scanf("%d %d",&n,&m);

memset(g,0x3F,sizeof(g));

for(i = 1; i <= n; i++) g[i][i] = 0;

for(i = 1; i <= m; i++)

{

scanf("%d %d %d",&a, &b, &len);

g[a][b] = g[b][a] = len;

}

Run the Floyd-Warshall algorithm to find the shortest paths between pairs of vertices.

floyd();

Let’s burt the vertex i (1 ≤ i ≤ n). Find the distance max from it to the farthest node. Find the smallest min value among all calculated max values.

min = 0x3F3F3F3F;

for(i = 1; i <= n; i++)

{

max = 0;

for(j = 1; j <= n; j++)

if (g[i][j] > max) max = g[i][j];

if (max < min) min = max, node = i;

}

Print the number of the node that should be set on fire and the minimum possible time min for burning all ropes.

printf("%d %d\n",node,min);